America has lottery fever, and the only prescription is more Powerball tickets. The jackpot for the nation’s largest lottery grew to $1.4 billion
over the weekend after Saturday night’s drawing produced no winners. So
with the jackpot now at ten figures, has it finally become
mathematically rational to purchase a Powerball lottery ticket?
Not quite, but it’s getting pretty close. In order to understand why it still doesn’t make pure mathematical or financial sense to purchase a $2 Powerball ticket, you really only need to know about two factors affecting the winner’s ultimate payout: state and federal income taxes, and the possibility of a split pot.
Before we get to those two issues, though, let’s briefly recap how Powerball works and how the basic probabilities of winning are calculated. To win the jackpot, you must get the correct red Powerball number and match each of the five white numbers. The white numbers don’t need to be in any particular order, just so long as you have all of them and the Powerball number (in geekspeak, the Powerball probabilities are calculated using combinations, not permutations). The winning lotto combination is drawn from 26 red Powerballs and 69 white balls. There are a total of 292,201,338 different Powerball combinations, but only one number can win the jackpot.
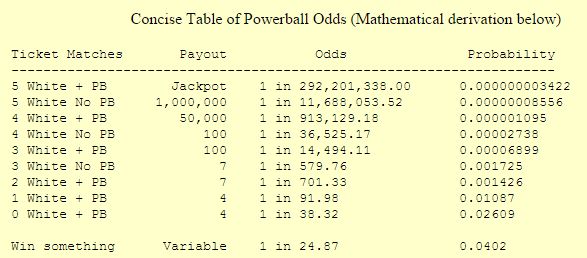
The jackpot, however, isn’t the only way to win money. You can win anywhere from $4 for guessing just the Powerball number correctly to $1 million for correctly guessing all of the five white balls while missing the red Powerball number. The probabilities of those different incomes obviously affect the game’s odds and slightly change the expected payout if you choose to purchase a $2 ticket. You can get a full run-down of the probabilities and the underlying math here if you’re interested. While the probability of winning the jackpot is exceedingly low—0.0000003422 percent, to be exact—your overall probability of winning something is just over 4 percent.
So with that math out of the way, we can get down to business calculating the expected payout of a ticket. In mathematical terms, the expected payout is a function of the total payouts for each scenario or outcome and the probabilities of each of those outcomes.
For example, imagine a game where you flip a fair coin, which would be a 50/50 proposition. If you get heads, you win $1. If you get tails, you receive $0. The expected payout of that game is $0.50: 50% x $1 for heads ($0.50) plus 50% x $0 for tails ($0.00), for a total of $0.50. As a pure mathematical matter, a risk-neutral person would happily play that game if it cost less than $0.50 to play.
Why? The net expected payout—the expected payout minus the cost to play—would be positive. If the cost to play exceeds the expected payout, it does not make financial sense to play. Because lotteries almost always have a ticket price that exceeds the expected payout, it rarely makes financial sense to buy a ticket.
While the current lump sum cash payout being advertised by Powerball is $868 million (the eye-popping number usually advertised is the annuity value paid out over 30 years, not the immediate lump sum payout), that’s not how much will end up in your pocket if you win. You’ll send 39.6 percent of that right back to the federal government in income taxes. And depending on which state you live in, you’ll have to send another hefty check to your state government.
As a result, instead of using the advertised lottery payout in our expected payout calculation, we have to use the after-tax payout to determine whether it’s really a good financial idea to buy a Powerball ticket. To make things simple tax-wise, we’ll assume you live in a state with no income tax and that you’ll pay the top federal marginal income tax rate of 39.6 percent. Using those assumptions and current jackpot cash payout estimates, you’ll take home $524 million after taxes.
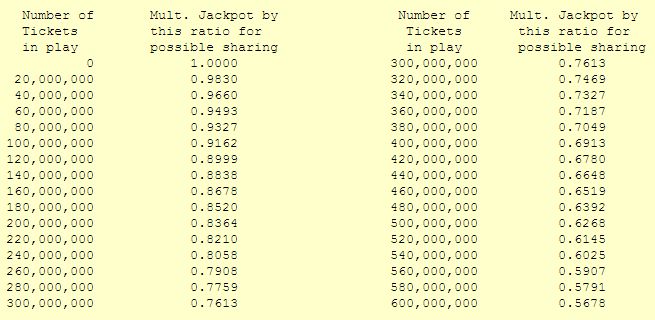
We can’t stop there, though. Because more than one person can win the Powerball jackpot, we have to take into account the probability of a split pot. The chances of a split pot increase as more and more people purchase lottery tickets. According to Powerball officials, over a billion dollars worth of tickets were sold over the weekend, meaning at least 500 million tickets were sold to hopeful buyers. If you use the split pot probability table shown below and use 500 million tickets as your benchmark, the probability of a split pot reduces the expected take-home amount by roughly 37 percent. So that $524 million after-tax expected payout needs to be bumped down to $328.6 million before we can calculate our expected payout.
To get the expected after-tax jackpot payout, you would then multiply that number by the probability of winning the jackpot, which is 1 divided by 292,201,338. What’s the end result? A whopping expected payout of $1.12…on a ticket that cost you $2. Once you add in the expected payouts from all the other potential Powerball prizes, that number increases to $1.32. And again, that assumes you live in a state with no income taxes.
So right now, given the advertised cash payout and the number of people playing, it does not make financial sense to purchase a Powerball ticket. That said, we’re not all that far off from a jackpot that might justify the purchase of a ticket. If the lump sum cash payout (not the annuity value) increases to $1.4 billion, and the number of tickets sold hovers around 500 million, the total expected payout of a $2 Powerball ticket will be $2.01, making the purchase of a ticket a rational decision in pure mathematical terms.
If we go another week or two without a Powerball winner, resulting in higher and higher lump sum jackpot amounts, we might finally reach a point where it actually makes financial sense to buy a Powerball ticket.
Not quite, but it’s getting pretty close. In order to understand why it still doesn’t make pure mathematical or financial sense to purchase a $2 Powerball ticket, you really only need to know about two factors affecting the winner’s ultimate payout: state and federal income taxes, and the possibility of a split pot.
Before we get to those two issues, though, let’s briefly recap how Powerball works and how the basic probabilities of winning are calculated. To win the jackpot, you must get the correct red Powerball number and match each of the five white numbers. The white numbers don’t need to be in any particular order, just so long as you have all of them and the Powerball number (in geekspeak, the Powerball probabilities are calculated using combinations, not permutations). The winning lotto combination is drawn from 26 red Powerballs and 69 white balls. There are a total of 292,201,338 different Powerball combinations, but only one number can win the jackpot.
The jackpot, however, isn’t the only way to win money. You can win anywhere from $4 for guessing just the Powerball number correctly to $1 million for correctly guessing all of the five white balls while missing the red Powerball number. The probabilities of those different incomes obviously affect the game’s odds and slightly change the expected payout if you choose to purchase a $2 ticket. You can get a full run-down of the probabilities and the underlying math here if you’re interested. While the probability of winning the jackpot is exceedingly low—0.0000003422 percent, to be exact—your overall probability of winning something is just over 4 percent.

So with that math out of the way, we can get down to business calculating the expected payout of a ticket. In mathematical terms, the expected payout is a function of the total payouts for each scenario or outcome and the probabilities of each of those outcomes.
For example, imagine a game where you flip a fair coin, which would be a 50/50 proposition. If you get heads, you win $1. If you get tails, you receive $0. The expected payout of that game is $0.50: 50% x $1 for heads ($0.50) plus 50% x $0 for tails ($0.00), for a total of $0.50. As a pure mathematical matter, a risk-neutral person would happily play that game if it cost less than $0.50 to play.
Why? The net expected payout—the expected payout minus the cost to play—would be positive. If the cost to play exceeds the expected payout, it does not make financial sense to play. Because lotteries almost always have a ticket price that exceeds the expected payout, it rarely makes financial sense to buy a ticket.
In the case of the Powerball lottery, the house
consists of the federal government and various state governments
administering the lottery.
The lottery, much like games at any casino, is heavily tilted in
favor of the house and against the player. In the case of the Powerball
lottery, the house consists of the federal government and various state
governments administering the lottery. That’s because of taxes, the
possibility of a split pot, and the fact that the advertised jackpot
will always be significantly lower than the ticket revenue collected.While the current lump sum cash payout being advertised by Powerball is $868 million (the eye-popping number usually advertised is the annuity value paid out over 30 years, not the immediate lump sum payout), that’s not how much will end up in your pocket if you win. You’ll send 39.6 percent of that right back to the federal government in income taxes. And depending on which state you live in, you’ll have to send another hefty check to your state government.
As a result, instead of using the advertised lottery payout in our expected payout calculation, we have to use the after-tax payout to determine whether it’s really a good financial idea to buy a Powerball ticket. To make things simple tax-wise, we’ll assume you live in a state with no income tax and that you’ll pay the top federal marginal income tax rate of 39.6 percent. Using those assumptions and current jackpot cash payout estimates, you’ll take home $524 million after taxes.
We can’t stop there, though. Because more than one person can win the Powerball jackpot, we have to take into account the probability of a split pot. The chances of a split pot increase as more and more people purchase lottery tickets. According to Powerball officials, over a billion dollars worth of tickets were sold over the weekend, meaning at least 500 million tickets were sold to hopeful buyers. If you use the split pot probability table shown below and use 500 million tickets as your benchmark, the probability of a split pot reduces the expected take-home amount by roughly 37 percent. So that $524 million after-tax expected payout needs to be bumped down to $328.6 million before we can calculate our expected payout.

To get the expected after-tax jackpot payout, you would then multiply that number by the probability of winning the jackpot, which is 1 divided by 292,201,338. What’s the end result? A whopping expected payout of $1.12…on a ticket that cost you $2. Once you add in the expected payouts from all the other potential Powerball prizes, that number increases to $1.32. And again, that assumes you live in a state with no income taxes.
So right now, given the advertised cash payout and the number of people playing, it does not make financial sense to purchase a Powerball ticket. That said, we’re not all that far off from a jackpot that might justify the purchase of a ticket. If the lump sum cash payout (not the annuity value) increases to $1.4 billion, and the number of tickets sold hovers around 500 million, the total expected payout of a $2 Powerball ticket will be $2.01, making the purchase of a ticket a rational decision in pure mathematical terms.
If we go another week or two without a Powerball winner, resulting in higher and higher lump sum jackpot amounts, we might finally reach a point where it actually makes financial sense to buy a Powerball ticket.
What a great day with such a great blogger like you. I stumbled upon your blog and it clicks I love it. Thank you for sharing this information. Have a great day!
ReplyDeletehttps://hpx7.com/ 바카라사이트
It was thinking about whether I could utilize this review on my other site, I will connect it back to your site though.Great Thanks. 먹튀
ReplyDeleteThere is so much in this article that I would never have thought of on my own. Your content gives readers things to think about in an interesting way. 파워볼사이트
ReplyDeleteI have read your article; it is very informative and helpful for me. I admire the valuable information you offer in your articles. Thanks for posting it 먹튀폴리스
ReplyDeleteGreat post. I found your website comprehensive for my needs. I truly like what you have acquired here, 안전놀이터
ReplyDeleteThanks for your post. I’ve been thinking about writing a very comparable post over the last couple of weeks. I’ll probably keep it short and sweet and link to this instead if thats cool. Thank 안전놀이터
ReplyDeleteExcellent, this article is really helpful. Mes doubles dans autres produits 토토사이트
ReplyDeleteTranslation companies are generally a safe decision, over individual freelance translators. A translation company found fairly easily online has to work to become established - especially with so much online competition 먹튀검증커뮤니티
ReplyDeleteHello I am so delighted I located your blog, I really located you by mistake, while I was watching on google for something else, Anyways I am here now and could just like to say thank for a tremendous post and a all round entertaining website. Please do keep up the great work. 먹튀검증
ReplyDeleteProfessional gutter cleaning company in London with over 10 years experience. We provide residential and commercial gutter cleaning, unblocking downpipes, gutter repair and soffit and fascia cleaning throughout Greater London 먹튀검증
ReplyDeleteI am incapable of reading articles online very often, but I’m happy I did today. It is very well written, and your points are well-expressed. I request you warmly, please, don’t ever stop writing 먹튀폴리스
ReplyDeleteYoure so cool! I dont suppose Ive read something like this before. So nice to seek out any person with some unique ideas on this subject. realy thank you for beginning this up. this website is one thing that’s needed on the web, somebody with a little originality 안전놀이터
ReplyDeleteYes i am totally agreed with this article and i just want say that this article is very nice and very informative article.I will make sure to be reading your blog more. You made a good point but I can't help but wonder, what about the other side? !!!!!!Thanks 토토사이트
ReplyDeleteWow, excellent post. I'd like to draft like this too - taking time and real hard work to make a great article. This post has encouraged me to write some posts that I am going to write soon 먹튀폴리스
ReplyDeleteReally impressive post. I read it whole and going to share it with my social circules. I enjoyed your article and planning to rewrite it on my own blog 슈어맨
ReplyDeleteThis specific is generally clearly basic and in addition exceptional truth alongside without a doubt reasonable and besides in fact valuable My business is seeking find ahead of time intended for this particular helpful stuff 먹튀폴리스
ReplyDeleteNice to be visiting your blog again, it has been months for me. Well this article that i've been waited for so long. I need this article to complete my assignment in the college, and it has same topic with your article. Thanks, great share. 파워볼사이트
ReplyDeleteThis is a wonderful article, Given so much info in it, These type of articles keeps the users interest in the website, and keep on sharing more ... good luck rooftop deck shade solutions
ReplyDeleteGood to become visiting your weblog again, it has been months for me. Nicely this article that i've been waited for so long. I will need this post to total my assignment in the college, and it has exact same topic together with your write-up. Thanks, good share. courtier immobilier Engel & Völkers
ReplyDeleteI’ve found every article I’ve read very helpful. Good one, and keep it going. courtier immobilier gatineau
ReplyDelete"I’m going to read this. I’ll be sure to come back. thanks for sharing. and also This article gives the light in which we can observe the reality. this is very nice one and gives indepth information. thanks for this nice article...
ReplyDelete" EBWaite
You've completed in excellent work. t suggest to my frtends ind personilly wtll certitnly dtgtt. t'm conftdent they'll be gitned from thts webstte 먹튀검증업체
ReplyDeleteThe information you have posted is very useful. The sites you have referred was good. Thanks for sharing digital marketing malta
ReplyDeletecvhi was just seeing if you minded a comment. i like your website and the thme you picked is super. I will be back. 메이저사이트 추천
ReplyDeleteThat's a really good post. Your writing is very interesting and entertaining me. 슬롯사이트
ReplyDeleteThis is my first time i visit here. I found so many entertaining stuff in your blog, especially its discussion. From the tons of comments on your articles, I guess I am not the only one having all the leisure here! Keep up the good work. I have been meaning to write something like this on my website and you have given me an idea. 메이저사이트 추천
ReplyDeleteusually, the best sounding ringtones are coming from paid ringtone donwload site 먹튀검증
ReplyDelete"Thank you for the auspicious writeup. It in fact was a amusement account it.
ReplyDeleteLook advanced to more added agreeable from you!" 먹튀폴리스
Appreciating the time and energy you put into your website and detailed information you present. It’s great to come across a blog every once in a while that isn’t the same outdated rehashed information. Excellent read! 먹튀폴리스
ReplyDeleteHi! This is my first visit to your blog! We are a team of volunteers and new initiatives in the same niche. Blog gave us useful information to work. You have done an amazing job 토토사이트
ReplyDelete